如图,椭圆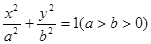 的一个 焦点是F(1,0),O为坐标原点.
的一个 焦点是F(1,0),O为坐标原点.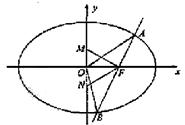
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线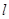 交椭圆于A、B两点,若直线
交椭圆于A、B两点,若直线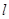 绕点F任意转动,恒有
绕点F任意转动,恒有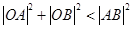 , 求
, 求 的取值范围.
的取值范围.
(本小题满分10分)
已知函数
(I)求函数 的最小正周期;
的最小正周期;
(I I)求函数
I)求函数 上的最大值与最小值。
上的最大值与最小值。
(本小题满分14分)
已知向量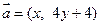 , 向量
, 向量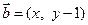 , 且
, 且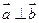 , 动点
, 动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B, 且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(本小题满分14分)
如图,过抛物线 上一点P(
上一点P(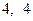 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(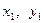 ),B(
),B( ).直线PA与PB的斜率存在且互为相反数,(1)求
).直线PA与PB的斜率存在且互为相反数,(1)求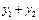 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.
(本小题满分14分)
已知动圆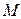 经过点
经过点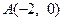 ,且与圆
,且与圆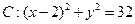 内切.
内切.
(1)求动圆圆心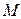 的轨迹
的轨迹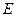 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点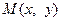 到定点B(1,0)的距离
到定点B(1,0)的距离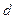 的最小值,并求
的最小值,并求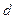 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.
(本小题满分14分)
(1)掷两颗骰子,其点数之和为4的概率是多少?
(2)甲、乙两人约定上午9点至12点在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,一小时之内如对方不来,则离去。如果他们二人在8点到12点之间的任何时刻到达约定地点的概率都是相等的,求他们见到面的概率。