(本小题满分14分)
已知动圆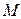 经过点
经过点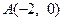 ,且与圆
,且与圆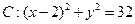 内切.
内切.
(1)求动圆圆心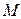 的轨迹
的轨迹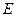 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点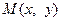 到定点B(1,0)的距离
到定点B(1,0)的距离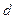 的最小值,并求
的最小值,并求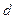 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.
设数列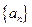 满足
满足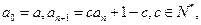 其中
其中 为实数,且
为实数,且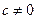
(Ⅰ)求数列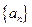 的通项公式
的通项公式
(Ⅱ)设 ,
,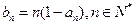 ,求数列
,求数列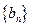 的前
的前 项和
项和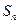 ;
;
(Ⅲ)若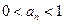 对任意
对任意 成立,证明
成立,证明
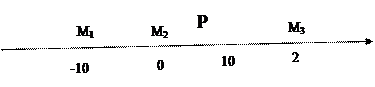
已知3台机器位于直线l上,机器所在的位置如下图所示,其中 M1 M2 ="10m," M2 M3 =20m;现要放置一台检验台P,用函数方法确定放在哪里可使检验台P到3台机器的距离和最小?
|




设函数 ,曲线
,曲线 在点
在点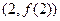 处的切线方程
处的切线方程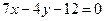 。
。
(1)求 的解析式;
的解析式;
(2)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线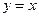 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
若 ,求函数f(x)=
,求函数f(x)=  的值域.
的值域.
(本小题满分13分)
已知函数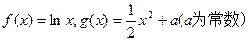 ,若直线
,若直线 与
与 的图象都相切,且
的图象都相切,且 与
与 的图象相切于定点
的图象相切于定点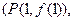
(1)求直线 的方程及a的值;
的方程及a的值;
(2)当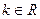 时,讨论关于x的方程
时,讨论关于x的方程 的实数解的个数.
的实数解的个数.