(本小题满分14分)椭圆 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=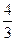 | ,P F2|=
| ,P F2|=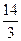 .
.
(I)求椭圆C的方程;
(II)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
已知函数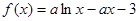 ,
,
①求函数 的单调区间。
的单调区间。
②若函数 的图象在点(2,
的图象在点(2, )处的切线的倾斜角为
)处的切线的倾斜角为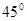 ,对任意的
,对任意的 ,函数
,函数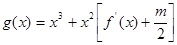 在区间
在区间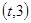 上总不是单调函数,求m取值范围
上总不是单调函数,求m取值范围
③求证:
已知抛物线C: 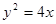 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线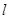 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量 在向量
在向量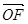 上的投影为n,且
上的投影为n,且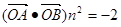 ,求直线
,求直线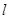 的方程。
的方程。
在平面直角坐标系中,已知某点 ,直线
,直线 .求证:点P到直线
.求证:点P到直线 的距离
的距离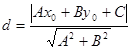
已知数列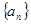 是公差为1的等差数列,
是公差为1的等差数列,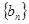 是公比为2的等比数列,
是公比为2的等比数列,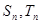 分别是数列
分别是数列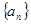 和
和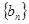 前n项和,且
前n项和,且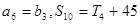
①分别求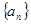 ,
,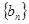 的通项公式。
的通项公式。
②若 ,求n的范围
,求n的范围
③令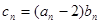 ,求数列
,求数列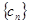 的前n项和
的前n项和 。
。
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是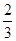 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望。
的分布列和数学期望。