(本小题满分12分)根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
| 社团 |
街舞 |
围棋 |
武术 |
| 人数 |
320 |
240 |
200 |
社团抽取的同学8人。
(Ⅰ) 求 的值和从“围棋”社团抽取的同学的人数;
的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率。
(本小题共14分)已知二次函数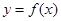 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为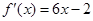 ,数列
,数列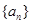 的前
的前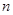 项和为
项和为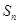 ,点
,点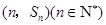 均在函数
均在函数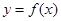 的图象上.
的图象上.
(1)求数列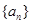 的通项公式;
的通项公式;
(2)设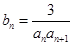 ,
,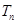 是数列
是数列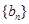 的前
的前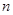 项和,求使得
项和,求使得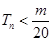 对所有
对所有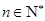 都成立的最小正整数
都成立的最小正整数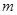 .
.
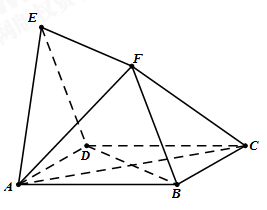
(本小题共14分)如图,四边形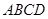 与
与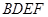 均为菱形,
均为菱形, 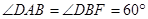 ,且
,且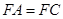 .
.
(Ⅰ)求证: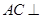 平面
平面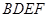 ;
;
(Ⅱ)求证: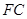 ∥平面
∥平面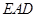 ;
;
(Ⅲ)求二面角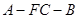 的余弦值.
的余弦值.
(本小题共13分)已知函数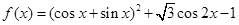 .
.
(1)求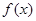 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求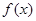 在区间
在区间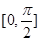 上的最大值和最小值.
上的最大值和最小值.
(本小题满分13分)设函数f(x)=x3–3ax2+3bx的图象与直线12x+y–1=0相切于点(1,–11).
(1)求a,b的值;
(2)求函数f (x)的单调区间.
(本小题共13分)如图,在四棱锥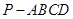 中,底面
中,底面 是矩形,
是矩形, 分别是
分别是 的中点,
的中点, 平面
平面 ,且
,且 ,
, .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明: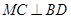 .
.