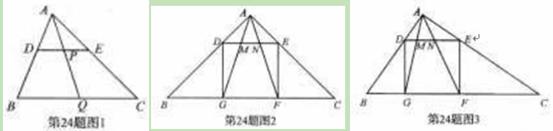
如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y(cm),其中0≤x≤2.5.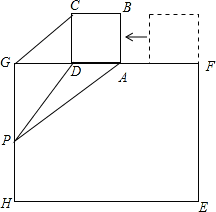
(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;
(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1-S2是常数;
(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.
某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结构;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下表为“1”)均为奇数的概率.
如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)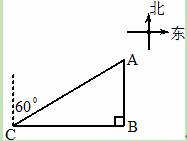
(1)计算: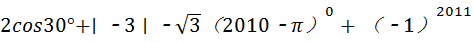 .
.
(2)解不等式组: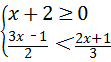 ,并写出该不等式组的最小整数解.
,并写出该不等式组的最小整数解.
如图1,抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.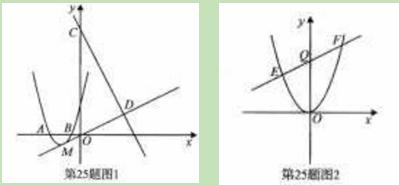
(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证: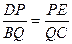 .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.