已知关于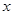 的一元二次方程
的一元二次方程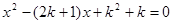 .
.
(1)求证:方程有两个不相等的实数根;
(2)若 的两边
的两边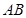 、
、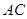 的长是方程的两个实数根,第三边
的长是方程的两个实数根,第三边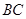 的长为
的长为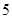 .当
.当 是等腰三角形时,求
是等腰三角形时,求 的值.
的值.
(·辽宁大连)在□ABCD中,点E、F在AC上,且∠ABE=∠CDF,
求证:BE=DF.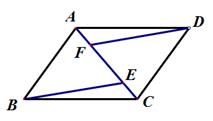
(·黑龙江绥化)如图1,在正方形ABCD中,延长BC至M ,使BM="DN" ,连接MN交BD延长线于点E.
(1)求证:BD+2DE= BM .
BM .
(2)如图2 ,连接BN交AD于点F ,连接MF交BD于点G.若AF:FD="1:2" ,且CM=2,则线段DG=_______.
(·黑龙江绥化)在平面直角坐标系xoy中 ,直线y="-x+3" 与x轴、y轴分别交于A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。
(·黑龙江省黑河市、齐齐哈尔市、大兴安岭)【8分】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
(·黑龙江哈尔滨)(本题8分)
如图1, 平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
