已知:BE⊥CD,BE=DE,BC=DA,求证:(1)△BEC≌△DAE(2)DF⊥BC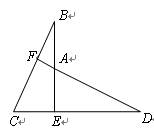
在图中作出点P,使得点P到C、D两点的距离相等,并且点P到OA、OB的距离也相等. (用尺规作图,保留作图痕迹,不写作法.)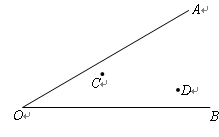
如图,在平面直角坐标系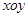 中,
中,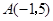 ,
,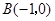 ,
,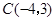 .
.
(1)求出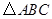 的面积.
的面积.
(2)在图中作出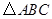 关于
关于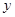 轴的对称图形
轴的对称图形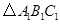 .
.
(3)写出点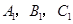 的坐标
的坐标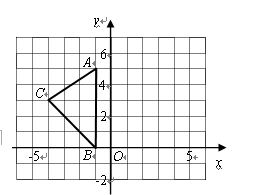
我省某地生产的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元.
当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可以加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须用15天的时间将这批蔬菜全部销售或加工完毕,因此,公司制定了三种可行方案:
方案一:将蔬菜全部进行精加工.
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接出售.
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好用15天完成.
你认为选择哪种方案获利最多?为什么?
已知方程组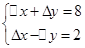 中,
中, 的系数部已经模糊不清,但知道其中□表示同一个数,△也表示同一个数,
的系数部已经模糊不清,但知道其中□表示同一个数,△也表示同一个数,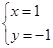 是这个方程组的解,你能求出原方程组吗?
是这个方程组的解,你能求出原方程组吗?