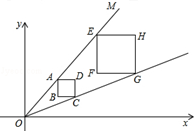
已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为 .
解一元二次方程: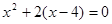
如图,已知抛物线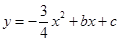 与坐标轴交于
与坐标轴交于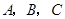 三点,点
三点,点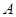 的横坐标为
的横坐标为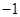 ,过点
,过点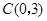 的直线
的直线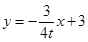 与
与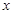 轴交于点
轴交于点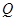 ,点
,点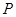 是线段
是线段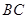 上的一个动点,
上的一个动点,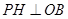 于点
于点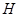 .若
.若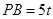 ,且
,且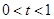 .
.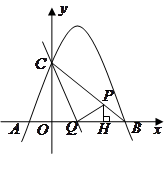
(1)求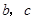 的值
的值
(2)求出点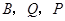 的坐标(其中
的坐标(其中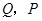 用含
用含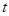 的式子表示):
的式子表示):
(3)依点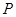 的变化,是否存在
的变化,是否存在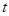 的值,使
的值,使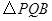 为等腰三角形?
为等腰三角形?
在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于D,F两点.(12分)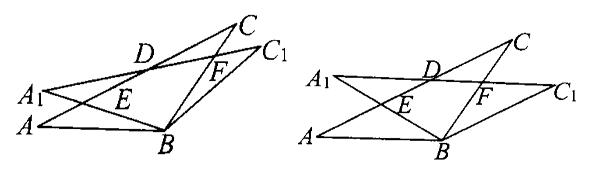
图(a)图(b)
(1)如图(a),观察并猜想,在旋转过程中,线段EA1与FC是怎样的数量关系?并证明你的结论;
(2)如图(b),当α=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
某商厦今年一月份销售额为60万元,二月份由于经营不善,销售额下降10%,以后改进管理,大大激发全体员工的积极性,月销售额大幅度上升,到四月份销售额猛增到96万元,求三、四月份平均每月增长的百分率是多少?(精确到0.1%)
如图,四边形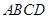 内接于⊙
内接于⊙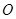 ,
,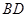 是⊙
是⊙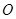 的直径,
的直径,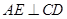 ,垂足为
,垂足为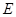 ,
, 平分
平分 .
.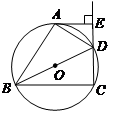
(1)求证: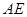 是⊙
是⊙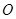 的切线;
的切线;
(2)若 ,求
,求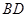 的长.
的长.