(本题13分)已知以椭圆C: 的短轴为直径,以原点为圆心的圆与直线
的短轴为直径,以原点为圆心的圆与直线 相切,且椭圆椭圆C的离心率为
相切,且椭圆椭圆C的离心率为 .
.
(1)求椭圆C的方程;
(2)若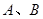 是椭圆C上的两点,且
是椭圆C上的两点,且 轴,
轴, ,连接直线
,连接直线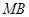 交椭圆C于另一点
交椭圆C于另一点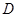 (不同于
(不同于 点),试分析直线
点),试分析直线 与
与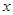 轴是否相交于定点?若是,求出定点坐标;若不是,请加以证明.
轴是否相交于定点?若是,求出定点坐标;若不是,请加以证明.
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1;③圆心到直线l:x-2y=0的距离为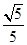 ,求该圆的方程.
,求该圆的方程.
如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若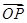 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).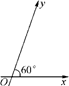
(1)若P点斜坐标为(2,-2),求P到O的距离|PO|;
(2)求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
若方程ax2+ay2-4(a-1)x+4y=0表示圆,求实数a的取值范围,并求出半径最小的圆的方程.
已知圆M过两点A(1,-1),B(-1,1),且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设P是直线3x+4y+8=0上的动点,PA′、PB′是圆M的两条切线,A′、B′为切点,求四边形PA′MB′面积的最小值.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连结BC并延长至D,使得CD=BC,求AC与OD的交点P的轨迹方程.