如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若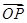 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).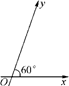
(1)若P点斜坐标为(2,-2),求P到O的距离|PO|;
(2)求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
如图,三棱锥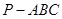 中,
中,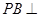 底面
底面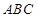 ,
, ,
,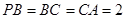 ,
, 为
为 的中点,点
的中点,点 在
在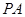 上,且
上,且 .
.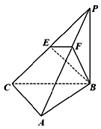
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女生被抽到的人数为X, 求X的分布列及数学期望E(X) .
附表及公式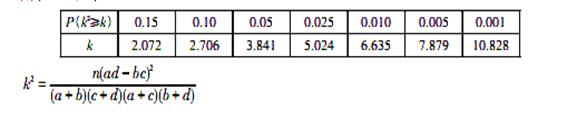
 中,角
中,角 所对边分别是
所对边分别是 ,
, ,
,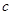 ,且
,且 .
.
(1)求 的值;
的值;
(2)若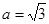 ,求
,求 面积的最大值.
面积的最大值.
选修4-5:不等式选讲。
已知函数 的解集为
的解集为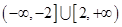 .
.
(1)求 的值;
的值;
(2)若 ,
,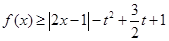 成立,求实数
成立,求实数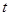 的取值范围.
的取值范围.
选修4-4:极坐标系与参数方程
已知曲线 的参数方程为
的参数方程为 (
( 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点, 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线 的极坐标方程,并说明其表示什么轨迹.
的极坐标方程,并说明其表示什么轨迹.
(2)若直线的极坐标方程为 ,求直线被曲线
,求直线被曲线 截得的弦长.
截得的弦长.