已知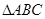 中,
中,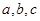 是三个内角
是三个内角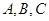 的对边,关于
的对边,关于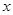 的不等式
的不等式
 的解集是空集.
的解集是空集.
(1)求角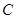 的最大值;
的最大值;
(2)若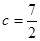 ,
, 的面积
的面积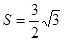 ,求当角
,求当角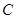 取最大值时,
取最大值时,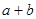 的值.[
的值.[
为了解某班关注NBA(美国职业篮球)是否与性别有关,对某班48人进行了问卷调查得到如下的列联表:
| 关注NBA |
不关注NBA |
合计 |
|
| 男生 |
6 |
||
| 女生 |
10 |
||
| 合计 |
48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为 .
.
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由;
(2)设甲,乙是不关注NBA的6名男生中的两人,丙,丁,戊是关注NBA的10名女生中的3人,从这5人中选取2人进行调查,求:甲,乙至少有一人被选中的概率.
答题参考
| P(K2≥k) |
0.10 |
0.05 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
6.635 |
7.879 |

)已知向量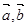 满足
满足 ,且
,且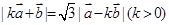 ,令
,令 .
.
(1)求 (用
(用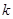 表示);
表示);
(2)当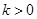 时,
时,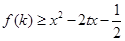 对任意的
对任意的 恒成立,求实数
恒成立,求实数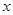 的取值范围。
的取值范围。
已知 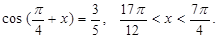
(1) 求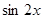 的值. (2)求
的值. (2)求  的值.
的值.
已知向量 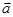 =(cos
=(cos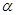 ,sin
,sin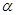 ),
),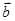 =(cos
=(cos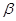 ,sin
,sin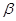 ),
),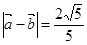 。
。
(1)求cos(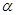 -
-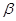 )的值;
)的值;
(2)若0<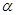 <
<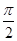 ,-
,-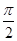 <
<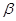 <0,且sin
<0,且sin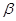 =-
=-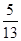 ,求sin
,求sin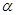 的值.
的值.