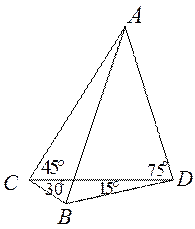(本小题满分14分)已知等差数列 的前
的前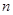 项和为
项和为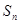 ,且
,且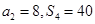 .数列
.数列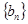 的前
的前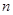 项和为
项和为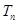 ,且
,且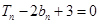 ,
,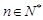 .
.
(Ⅰ)求数列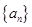 ,
,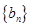 的通项公式;
的通项公式;
(Ⅱ)设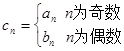 , 求数列
, 求数列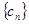 的前
的前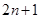 项和
项和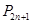 .
.
(本小题满分14分)
已知集合 ,集合
,集合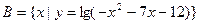 ,
,
集合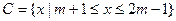 .
.
(1)求 ;
;
(2)若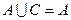 ,求实数
,求实数 的取值范围.
的取值范围.
函数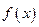 是定义在
是定义在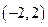 上的奇函数,且在
上的奇函数,且在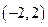 上单调递减,
上单调递减,
若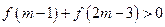 ,求
,求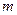 的取值范围。
的取值范围。
本题满分14分)
已知函数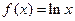 ,
,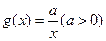 ,设
,设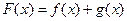 .
.
(Ⅰ)求函数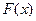 的单调区间;
的单调区间;
(Ⅱ)若以函数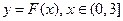 图像上任意一点
图像上任意一点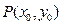 为切点的切线的斜率
为切点的切线的斜率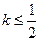 恒成立,求实数
恒成立,求实数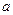 的最小值;
的最小值;
(Ⅲ)是否存在实数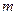 ,使得函数
,使得函数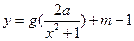 的图像与函数
的图像与函数 的图像恰有四个不同的交点?若存在,求出实数
的图像恰有四个不同的交点?若存在,求出实数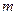 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
本题满分13分)
已知不等式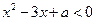 的解集为
的解集为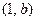
(Ⅰ)求实数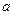 、
、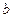 的值;
的值;
(Ⅱ)若函数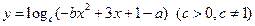 在区间
在区间 的值恒小于1,求
的值恒小于1,求 的取值范围.
的取值范围.
.(本题满分12分)
某单位在抗雪救灾中,需要在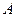 、
、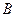 两地之间架设高压电线,测量人员在相距
两地之间架设高压电线,测量人员在相距
6000米的 、
、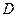 两地(
两地(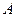 、
、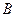 、
、 、
、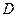 在同一平面上),测得
在同一平面上),测得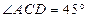 ,
,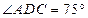 ,
,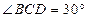 ,
,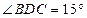 (如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是
(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是 、
、 距离的
距离的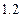 倍,问施工单
倍,问施工单
位至少应该准备多长的电线?(精确到小数点后1位;参考数据: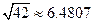 )
)