(1)如图1,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△AEG的面积。
(2)如图2,正方形ABCD和CEFG的边长分别为m、n,用含m、n的代数式表示△DBF的面积。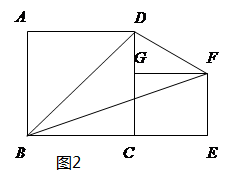
(3)如图,正方形ABCD、正方形CEFG和正方形MNHF的位置如图所示,点G在线段AN上,已知正方形CEFG的边长为6,则△AEN的面积为 (请直接写出结果,不需要过程)
计算:(a﹣b)(a2+ab+b2)
某小区规划在长30米,宽20米的长方形场地上,修建1横2纵三条宽均为x米的甬道,其余部分为绿地,请求出该绿地的面积.(用含x的式子表示)
(1)|﹣ |+
|+ +
+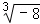 .
.
(2)(2x+y)(x﹣y).
计算:(3x+2)(7x﹣5)
先观察下列各式,再解答后面问题:(x+5)(x+6)=x2+11x+30;(x﹣5)(x﹣6)=x2﹣11x+30;(x﹣5)(x+6)=x2+x﹣30;(x+5)(x﹣6)=x2﹣x﹣30;
(1)乘积中的一次项系数、常数项与两因式中的常数项有何关系?
解:乘积中的一次项系数是:;乘积中的常数项是:.
(2)根据以上各式呈现的规律,用公式表示出来.
解:(x+a)(x+b)=.