（本题8分）在一个不透明的口袋里装有若干个质地相同的红球, 为了估计袋中红球的数量，某学习小组做了摸球实验, 他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色, 再把它放回袋中, 多次重复摸球. 下表是多次活动汇总后统计的数据：
| 摸球的次数S |
150 |
200 |
500 |
900 |
1000 |
1200 |
| 摸到白球的频数n |
51 |
64 |
156 |
275 |
303 |
361 |
| 摸到白球的频率 |
0.34 |
0.32 |
0.312 |
0.306 |
0.303 |
0.301 |
（1）请估计：当摸球次数S很大时, 摸到白球的频率将会接近 ；
假如你去摸一次，你摸到红球的概率是 ；（精确到0.1）.
（2）试估算口袋中红球有多少只?
阅读下面材料：如图，点A、B在数轴上分别表示有理数a、b，则A、B两点之间的距离可以表示为|a-b|．
根据阅读材料与你的理解回答下列问题：
（1）数轴上表示3与-2的两点之间的距离是 ．
（2）数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 ．
（3）代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离；
若|x+8|=5，则x= ．
（4）求代数式|x+1008|+|x+504|+|x-1007|的最小值．
某修路小组乘车从A地出发记为0，在东西走向的公路上检修公路，如果规定向东行驶为正，向西行驶为负，一天中行驶记录如下：（单位：千米）
-4，+7，-9，+8，+6，-4，-3
（1）求收工时在A地的 面方向？距A地 千米？
（2）该小组离A地最远时是 千米？
（3）若汽车每千米耗油0．3升，问从A地出发到收工回A地汽车共耗油多少升？
把下列各数的序号填入相应的横线上：
①-0．78，②5，③+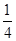
，④8．47，⑤-10，⑥-
，⑦0，⑧
，⑨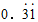
，⑩2．121121112…
整数有____________________________ ；（填序号）
分数有____________________________；（填序号）
有理数有___________________________；（填序号）
无理数有___________________________；（填序号）
在数轴上画出表示下列各数的点，并把它们从小到大排列；
－4，0．5，3，－2．
如图，已知正方形ABCD中，边长为10cm，点E在AB边上，BE=6cm．如果点P在线段BC上以2cm/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动，设运动的时间为t秒，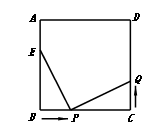
①CP的长为 cm（用含t的代数式表示）；
②若点Q的运动速度与点P的运动速度相等，经过2秒后，△BPE与△CQP是否全等？请说明理由．
③若点Q的运动速度与点P的运动速度不相等，△BPE与△CQP能否全等，若能全等，求出点Q的运动速度，若不能全等，请说明理由．