如图所示,已知OABC是-张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且0A=15,0C=9,在边AB上选取-点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.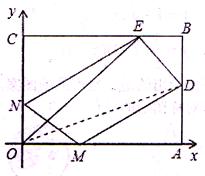
(1)求DE所在直线的解析式;
(2)设点P在x轴上,以点O、E、P为顶点的三角形是等腰三角形,问这样的点P有几个?并求出所有满足条件的点P的坐标;
(3)在x轴、y轴上是否分别存在点M、N,使四边形MNED的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由。
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,RtA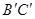 可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段
可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段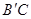 的长为_________________.
的长为_________________.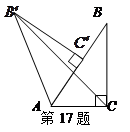
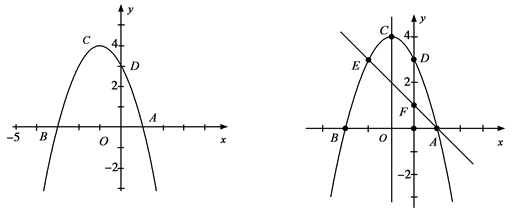
如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(-3,0)两点,与y轴交于点D(0,3)求这个抛物线的解析式
如图②,过点A的直线与抛物线交于点E,交
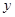 轴于点F,其中点E的横坐标为-2,若直线
轴于点F,其中点E的横坐标为-2,若直线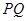 为抛物线的对称轴,点G为直线
为抛物线的对称轴,点G为直线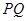 上的一动点,则
上的一动点,则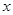 轴上是否存在一点H,使
轴上是否存在一点H,使 四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
图①图②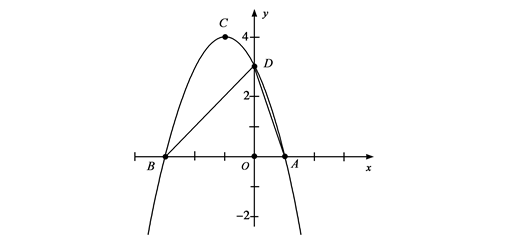
图③
探究(1)在图①中,已知线段AB、CD,点E、F分别为线段AB、CD的中点.
①若A(-2,0),B(4,0),则E点的坐标为;
②若C(-3,3),D(-3,-1),则F点的坐标为;
图①图②在图②中,已知线段AB的端点坐标为A
 求出图中AB的中点D的坐标(用含
求出图中AB的中点D的坐标(用含 的代数式表示),并给出求解过程.
的代数式表示),并给出求解过程.
归纳无论线段AB处于指定坐标系中的哪个位置,当其端点坐标为A AB中点为
AB中点为 时,
时, ,
,  .(不必证明)
.(不必证明)
运用已知如图③,一次函数 与反比例函数
与反比例函数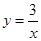 的图象交点为A,B.
的图象交点为A,B.
①求出交点A,B的坐标;
②若以A,O,B,P为顶点的四边形
是平行四边形,请利用上面的结论求出顶点P的坐标]
2011年3月10日,我国云南盈江县发生了5.8级的地震,在地震中某学校的课桌损坏严重,为了尽快的复课,该校有560张课桌急需维修,A工程队先维修一天,又请B工程队前来帮助,且B队平均每天比A队多修24张课桌,按照这样的工作效率进行,A、B两队需合作6天才能维修完剩下的课桌.求工程队A平均每天维修课桌的张数
A、B两队按计划合作施工2天,由于余震,学校又清理出需要维修的课桌198张,为了按时完成任务,学校又请来C工程队,A、C队的工作效率相同,且三个工程队决定从第3天开始,各自都提高工作效率,B队提高的工作效率是A、C队提高的2倍,这样他们至少还需要3天才能完成整个维修任务.求工程队A提高工作效率后平均每天多维修课桌的张数的取值范围.
如图,在梯形 中,
中, ,对角线
,对角线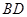 平分
平分 ,
, 的平分线
的平分线 交
交 于
于 分别是
分别是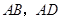 的中点.
的中点.求证:

当
 与
与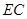 满足怎样的数量关系时,
满足怎样的数量关系时,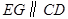 ?并说明理由.
?并说明理由.