如图所示,菱形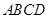 的顶点
的顶点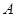 、
、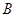 在
在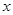 轴上,点
轴上,点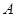 在点
在点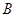
的左侧,点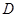 在
在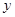 轴的正半轴上,
轴的正半轴上,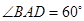 ,点
,点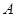 的坐标为(-2,0).
的坐标为(-2,0). 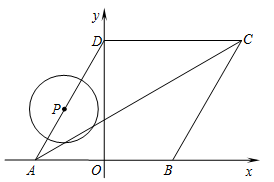
(1)求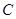 点的坐标;
点的坐标;
(2)求直线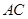 的函数关系式;
的函数关系式;
(3)动点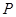 从点
从点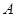 出发,以每秒1个单位长度的速度,按照
出发,以每秒1个单位长度的速度,按照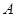 →
→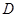 →
→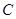 →
→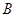 →
→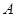 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为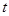 秒.求
秒.求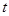 为何值时,以点
为何值时,以点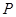 为圆心、以1为半径的圆与对角线
为圆心、以1为半径的圆与对角线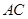 相切?
相切?
在一次数学游戏中,老师在 三个盘子里分别放了一些糖果,糖果数依次为
三个盘子里分别放了一些糖果,糖果数依次为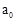 ,
,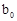 ,
, ,记为
,记为 (
(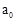 ,
,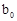 ,
, ).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.
).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.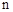 次操作后的糖果数记为
次操作后的糖果数记为 (
(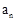 ,
, ,
, ).
).
(1)若 (4,7,10),则第_______次操作后游戏结束;
(4,7,10),则第_______次操作后游戏结束;
(2)小明发现:若 (4,8,18),则游戏永远无法结束,那么
(4,8,18),则游戏永远无法结束,那么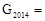 ________.
________.
对于平面直角坐标系xOy中的点P(a,b),若点 的坐标为(
的坐标为( ,
, )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为 (1+
(1+ ,
, ),即
),即 (3,6).
(3,6).
(1)①点P 的“2属派生点”
的“2属派生点”  的坐标为____________;
的坐标为____________;
②若点P的“k属派生点”  的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为 点,且△
点,且△ 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;
(3)如图, 点Q的坐标为(0, ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
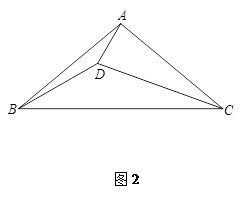
在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为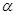 ,且
,且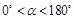 ,连接AD、BD.
,连接AD、BD.
(1)如图1,当∠BAC=100°,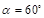 时,∠CBD 的大小为_________;
时,∠CBD 的大小为_________;
(2)如图2,当∠BAC=100°, 时,求∠CBD的大小;
时,求∠CBD的大小;
(3)已知∠BAC的大小为m(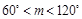 ),若∠CBD 的大小与(2)中的结果相同,请直接写出
),若∠CBD 的大小与(2)中的结果相同,请直接写出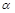 的大小.
的大小.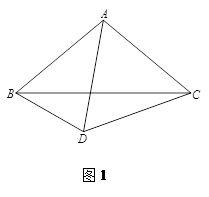
在平面直角坐标系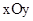 中,二次函数
中,二次函数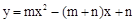 (
( )的图象与
)的图象与 轴正半轴交于A点.
轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
阅读下面材料:
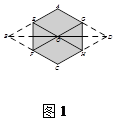
在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,
①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为_________;
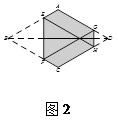
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长_________(填“改变”或“不变”).
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.
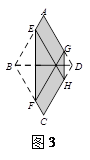
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为_________;
(2)如图4,若∠ABC的大小为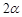 ,则六边形AEFCHG的周长可表示为________.
,则六边形AEFCHG的周长可表示为________.