已知圆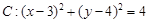 ,
,
(Ⅰ)若直线 过定点
过定点 (1,0),且与圆
(1,0),且与圆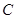 相切,求
相切,求 的方程;
的方程;
(Ⅱ)若圆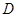 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆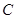 外切,求圆
外切,求圆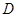 的方程.
的方程.
如图,在 ABC中,
ABC中,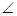 C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且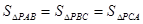 ,
,
(Ⅰ)建立适当的坐标系求出P的坐标;
(Ⅱ)求证:│PA│2+│PB│2=5│PC│2
(Ⅲ)若a+2b=2,求以PA,PB,PC分别为直径的三个圆的面积之和的最小值,并求出此时的b值.
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1;③圆心到直线l:x-2y=0的距离为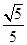 ,求圆的方程.
,求圆的方程.
(Ⅰ)求经过点(1,-7)与圆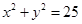 相切的切线方程.
相切的切线方程.
(Ⅱ)直线 经过点P(5,5)且和圆C:
经过点P(5,5)且和圆C: 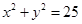 相交,截得弦长为
相交,截得弦长为 ,求
,求 的方程.
的方程.
已知圆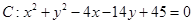 及点
及点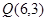 .
.
(1)若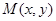 为圆
为圆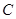 上任一点,求
上任一点,求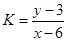 的最大值和最小值;
的最大值和最小值;
(2)已知点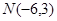 ,直线
,直线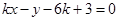 与圆C交于点A、B.当
与圆C交于点A、B.当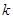 为何值时
为何值时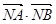 取到最小值。
取到最小值。
已知圆M过定点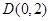 ,圆心M在二次曲线
,圆心M在二次曲线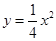 上运动
上运动
(1)若圆M与y轴相切,求圆M方程;
(2)已知圆M的圆心M在第一象限, 半径为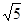 ,动点
,动点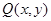 是圆M外一点,过点
是圆M外一点,过点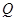 与 圆M相切的切线的长为3,求动点
与 圆M相切的切线的长为3,求动点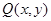 的轨迹方程;
的轨迹方程;