已知指数函数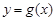
满足：
，定义域为
的函数
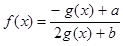是奇函数。
（1）求
，
的值；
（2）判断函数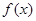
的单调性并用定义加以证明；
（3）若对任意的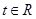
，不等式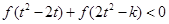
恒成立，求实数
的取值范围。
三角形ABC中，内角A、B、C所对的边a、b、c成公比小于1的等比数列，且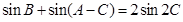
.（1）求内角B的余弦值；（2）若
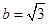，求三角形
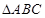的面积.
已知函数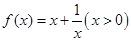
，以点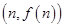
为切点作函数图像的切线
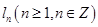，直线
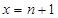与函数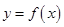
图像及切线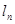
分别相交于
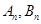，记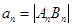
．
（1）求切线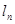的方程及数列
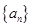的通项；
（2）设数列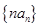
的前
项和为
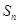，求证：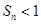
．
已知
的三个顶点都在抛物线
上，且抛物线的焦点
满足
，若
边上的中线所在直线
的方程为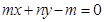
（
为常数且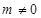
）．
（1）求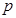
的值；
（2）
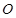为抛物线的顶点，
，
，
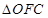的面积分别记为
，
，
，求证：
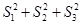为定值．
已知函数
．
（1）求证：
时，
恒成立；
（2）当
时，求
的单调区间．
如图，在多面体ABCDEF中，底面ABCD是梯形，且AD=DC=CB=
AB．直角梯形ACEF中，
，
是锐角，且平面ACEF⊥平面ABCD．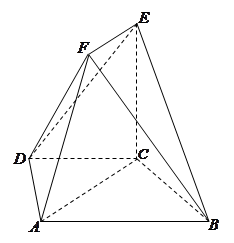
（1）求证：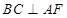
；
（2）试判断直线DF与平面BCE的位置关系，并证明你的结论．