有如图所示的一块地，已知AD=4米，CD=3米，
，AB=13米，BC=12米．
（1）试判断以点A、点B、点C为顶点的三角形是什么三角形?并说明理由．
（2）求这块地的面积．
（本题6分）先化简再求值：
2（3a2﹣ab）﹣3（2a2﹣ab），其中a=﹣2，b="3" 。
已知点A（8，0），B（0，6），C（0，—2），连结AB，点P为直线AB上一动点，过点P、C的直线
与AB及y轴围成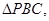
如图。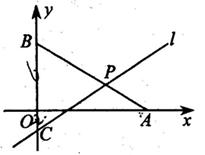
（1）求直线AB的解析式。
（2）如果PB=PC，求此
时点P的坐标。（3）点P在直线AB上运动，是否存在这样的点P，使得
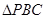的面积等于
的面积？若存在，请求出此时直线的解析式；若不能，请说明理由。
(12分)某公司在A、B两地分别有库存机器16台和12台，现要运往甲、乙两地，其中甲地15台，已地13台，从A地运一台到甲地的运费为500元，到乙地的运费为400元，从B地运一台到甲地的运300元，到乙地为600元，公司应怎样设计调运方案，能使这些机器的总运费最省？最省运费是多少？（设从A运到甲地的机器为X台，总运费为Y元）。
、(8分)已知一次函数y=Kx+b的图象过点(3，5)与(－4，－9)，（1）求这个一次函数解析式。
（2）利用函数图象求当x为何值时，y>0。
(8分)已知：如图，AB＝AE，BC＝ED，AF⊥CD且F是CD的中点，
求证：∠B＝∠E．