（本题12分）如图（1），在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C（0，m），A（n，m），且（m–4）2+n2–8n=–16，过C点作∠ECF分别交线段AB、OB于E、F两点．
（1）求A点的坐标．
（2）若OF+BE=AB，求证：CF=CE．
（3）如图（2），若∠ECF=45°，给出两个结论：OF+AE–EF的值不变；OF+AE+EF的值不变．其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值．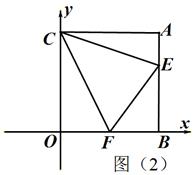
如图，C为以AB为直径的⊙O上一点，AD和过点C的切线互相垂直，垂足为点D．
（1）求证：AC平分∠BAD；
（2）若CD＝3，AC＝
，求⊙O 的半径长．
如图，在平面直角坐标系中，反比例函数
（
＞0）的图象和矩形ABCD的第一象限，AD平行于轴，且AB＝2，AD＝4，点A的坐标为（2，6） ．
（1）直接写出B、C、D三点的坐标；
（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．
在所给的5×5方格中，每个小正方形的边长都是1．按要求画平行四边形，
（1）在图甲中，画出一个平行四边形，使其有一个内角为45°且它的四个顶点在方格的顶点上．
（2）在图乙中，画出一个平行四边形（非特殊的平行四边形），使其周长为整数且它的四个顶点在方格的顶点上．
（3）在图丙中，画出一个平行四边形，使其面积为6且它的四个顶点以及对角线交点都在方格的顶点上．
将背面相同，正面分别标有数字1，2，3，4的四张卡片洗匀后，背面朝上放在桌面上．
（1）从中随机抽取一张卡片，求该卡片正面的数字是奇数的概率；
（2）先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是3的倍数的概率是多少？请用树状图或列表法加以说明．
先化简，再求值：
，其中
．