如图,在平面直角坐标系中,反比例函数 (
( >0)的图象和矩形ABCD的第一象限,AD平行于
>0)的图象和矩形ABCD的第一象限,AD平行于 轴,且AB=2,AD=4,点A的坐标为(2,6) .
轴,且AB=2,AD=4,点A的坐标为(2,6) .
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
已知双曲线 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.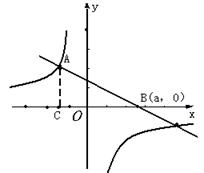
(1)求双曲线 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
南昌市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
| 销售额(万元) |
17 |
19 |
20 |
21 |
25 |
26 |
28 |
30 |
| 频数(人数) |
1 |
1 |
3 |
3 |
2 |
2 |
(2)上述数据中,众数是万元,中位数是万元,平均数是万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
某幼儿园在六一儿童节购买了一批牛奶.如果给每个小朋友分5盒;则剩下38盒,如果给每个小朋友分6盒,则最后小朋友不足5盒,但至少分得1盒.问:该幼儿园至少有多少名小朋友?最多有多少名小朋友.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;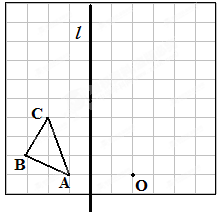
(1)先作△ABC关于直线 成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.