如图，二次函数y= -x2+ax+b的图象与x轴交于A（-
，0）、B（2，0）两点，且与y轴交于点C.
（1）求该拋物线的解析式，并判断△ABC的形状；
（2）在x轴上方的拋物线上有一点D，且以A、C、D、B四点为顶点的四边形是等腰梯形，请直接写出D点的坐标；
（3）在拋物线上存在点P，使得以A、C、B、P四点为顶点的四边形是直角梯形，求出P点的坐标.
先化简，再求值：(a-2+
)÷(a2+1)，其中a=
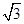-2.
解方程：(1) 3x2=4x
（2）m2－3m＋1＝0
（3）9(x－1)2－(x＋2)2＝0.
计算
(1)
（2）
（3）
如图，△ABC中,∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按
的路径运动，且速度为每秒1㎝，设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长。
(2)问t为何值时，△BCP为等腰三角形？
(3)另有一点Q，从点C开始，按
的路径运动，且速度为每秒2㎝，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动。当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
折叠矩形纸片ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm。
(1)求BF的长;（2）求折痕AE的长.