(本小题共12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=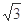 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(1)当点E为BC的中点时, 证明EF//平面PAC;
(2)求三棱锥E-PAD的体积;
(3)证明:无论点E在边BC的何处,都有PE AF.
AF.
已知△AOB的一个顶点为抛物线y2=2x的顶点O,A、B两点都在抛物线上,且∠AOB=90°.
(1)证明直线AB必过一定点;
(2)求△AOB面积的最小值.
已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为 ,并且与直线y=
,并且与直线y=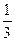 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为- ,求这个双曲线的方程.
,求这个双曲线的方程.
如图所示,过双曲线x2- =1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.
=1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.
经过双曲线x2- =1的左焦点F1作倾斜角为
=1的左焦点F1作倾斜角为 的弦AB,求:
的弦AB,求:
(1)|AB|;
(2)△F2AB的周长(F2为右焦点).
已知抛物线y2=x上存在两点关于直线l:y=k(x-1)+1对称,求实数k的取值范围.