(本题8分)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400
平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
(1)“地球一小时”是世界自然基金会在2007年提出的一项倡议.号召个人、社区、企业和政府在每年3月最后一个星期六20时30分—21时30分熄灯一小时,旨在通过一个人人可为的活动,让全球民众共同携手关注气候变化,倡导低碳生活.中国内地去年和今年共有119个城市参加了此项活动,且今年参加活动的城市个数比去年的3倍少13个,问中国内地去年、今年分别有多少个城市参加了此项活动.
(2)某中学2012年通过“废品回收”活动筹集钱款资助山区贫困中、小学生共23名,资助一名中学生的学习费用需a元,一名小学生的学习费用需b元,各年级学生筹款数额及用其恰好资助中,小学生人数的部分情况如下表:
| 年级 |
筹款数额(元) |
资助贫困中学生人数(名) |
资助贫困小学生人数(名) |
| 初一年级 |
4000 |
2 |
4 |
| 初二年级 |
4200 |
3 |
3 |
| 初三年级 |
7400 |
①求a,b的值;
②初三年级学生筹集的款项解决了其余贫困中小学生的学习费用,求出初三年级学生资助的贫困中、小学生人数。
计算
(1)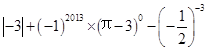 ;
;
(2) ;
;
(3)先化简,再求值:已知 ,求
,求 的值.
的值.
(1)解不等式 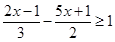 ,并把它的解集在数轴上表示出来
,并把它的解集在数轴上表示出来
(2)解不等式组 ,并在数轴上表示解集。
,并在数轴上表示解集。
解方程组:
(1)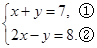
(2)
如果一条抛物线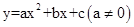 与
与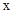 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是三角形;
(2)如图,△OAB是抛物线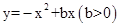 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.