如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
, ,求证:
,求证: ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
如果随机变量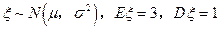 ,则
,则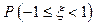 等于()
等于()
A.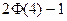 |
B.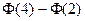 |
C.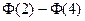 |
D.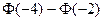 |
灯泡厂生产的白炽灯寿命ξ(单位:h),已知ξ~N(1000,302),要使灯泡的平均寿命为1000h的概率为99.7%,问灯泡的最低使用寿命应控制在多少小时以上?
某物体的温度 (
( )是一个随机变量,已知
)是一个随机变量,已知 ,又随机变量
,又随机变量 (
( )
)
满足 ,求
,求 的概率密度。
的概率密度。
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(Ⅰ)求3个旅游团选择3条不同的线路的概率;
(Ⅱ)求选择甲线路旅游团数的分布列和期望.
次体能测试中,规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为 (假定每次通过率相同)
(假定每次通过率相同)
(1) 求运动员甲参加测试的次数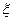 的分布列及数学期望;
的分布列及数学期望;
(2) 求运动员甲最多参加两次测试的概率(精确到 )
)