如图所示，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．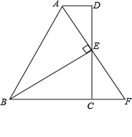
求证：（1）FC=AD；（2）AB=BC+AD．
已知，二次函数的表达式为
．写出这个函数图象的对称轴和顶点坐标，并求图象与
轴的交点的坐标
计算：
宾馆厨房的桌子上整齐叠放着若干只形状一样的碗，它的主视图如下，请你画出它的俯视图。设叠放这种碗
只叠放高度为
厘米，经实验发现，当叠放这种碗5只时，叠放高度为12厘米；当叠放这种碗8只时，叠放高度为15.6厘米。求（厘米）与（只）之间的函数关系，并指出这种碗的深度是多少？
解方程： 
.
设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下
表：(6分)
| d、a、r之间关系 |
公共点的个数 |
| d＞a＋r |
|
| d＝a＋r |
|
| a－r＜d＜a＋r |
|
| d＝a－r |
|
| d＜a－r |
所以，
当r＜a时，⊙O与正方形的公共点的个数可能有 个；
（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：(5分)
| d、a、r之间关系 |
公共点的个数 |
| d＞a＋r |
|
| d＝a＋r |
|
| a≤d＜a＋r |
|
| d＜a |
所以，当r＝a时，⊙O与正方形的公共点个数可能有 个；
（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝
a；(5分)