在正方形网格中建立如图所示的平面直角坐标系,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题。
(1)画出△ABC关于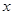 轴对称的△A1B1C1。
轴对称的△A1B1C1。
(2)画出△ABC关于原点对称的△A2B2C2。
(3)将△ABC绕点B逆时针旋转900,画出旋转后的A3BC3。
(4)求△A1A2A3的面积。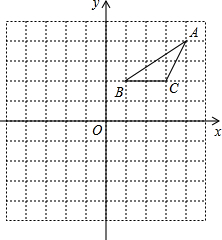
已知等腰三角形的底边长为9,腰是方程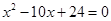 的一个根,求这个三角形的周长.
的一个根,求这个三角形的周长.
解下列方程:
(1)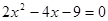 (用配方法解)
(用配方法解)
(2) 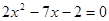
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).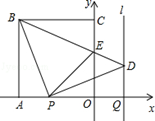
(1)∠PBD的度数为_____,点D的坐标为______ (用t表示);
(2)求证:PE=AP+CE
(3)当t为何值时,△PBE为等腰三角形?
阅读材料:用配方法求最值.已知x,y为非负实数,
∵x+y﹣2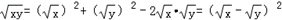 ≥0
≥0
∴x+y≥2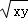 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y=x+ +4的最小值.
+4的最小值.
解: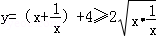 +4=6,当x=
+4=6,当x= ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y=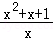 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为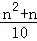 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
今年圣诞节前夕,小明、小丽两位同学到某超市调研一种袜子的销售情况,这种袜子的进价为每双1元,请根据小丽提供的信息解决小明提出的问题.
