已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．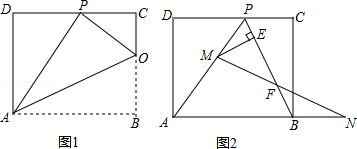
（1）如图1，已知折痕与边BC交于点O，连结AP、OP、OA．
①求证：△OCP∽△PDA；
②若△OCP与△PDA的面积比为1：4，求边AB的长；
（2）若图1中的点P恰好是CD边的中点，求∠OAB的度数；（提示：直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角为300）
（3）如图2，
，擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．
某区八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中抽取了200名学生的得分进行统计．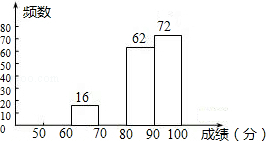
| 成绩x |
频数 |
频率 |
| 50≤x＜60 |
10 |
|
| 60≤x＜70 |
16 |
0.08 |
| 70≤x＜80 |
0.02 |
|
| 80≤x＜90 |
62 |
|
| 90≤x＜100 |
72 |
0.36 |
请你根据不完整的表格，回答下列问题：
（1）补全频率分布直方图；
（2）若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”？如果随机抽查一名参赛学生的成绩等级，则这名学生的成绩等级哪一个等级的可能性大？请说明理由．
如图，平面直角坐标系中，直线
与x轴交于点A，与双曲线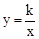
在第一象限内交于点B，BC丄x轴于点C，OC=2AO．求双曲线的解析式．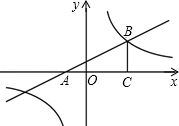
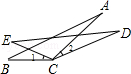
如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10千米，∠A=30°，∠B=45°．则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果保留根号）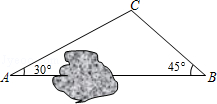
某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分，小明得分要超过90分，他至少要答对多少道题？
如图，CD=CA，∠1=∠2，EC=BC，求证：DE=AB．