(本小题满分12分)已知点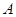 、
、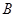 是椭圆
是椭圆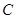 :
: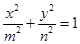 (
(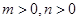 )与直线
)与直线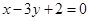 的交点.点
的交点.点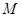 是
是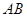 的中点,且点
的中点,且点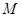 的横坐标为
的横坐标为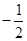 .若椭圆
.若椭圆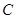 的焦距为
的焦距为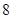 椭圆
椭圆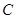 的方程。
的方程。
已知等差数列{an}的前n项和为Sn,公差d≠0,且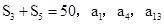 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)设 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
在△ABC中,角A,B,C所对的边为a,b,c,已知 a=2bsinA, .
.
(1)求B的值;
(2)若△ABC的面积为 ,求a,b的值.
,求a,b的值.
已知函数 的最大值是1,其图像经过点
的最大值是1,其图像经过点 。
。
(1)求 的解析式;
的解析式;
(2)已知 ,且
,且 求
求 的值.
的值.
设两向量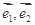 满足
满足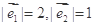 ,
,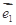 、
、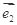 的夹角为
的夹角为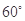 ,
,
(1)试求
(2)若向量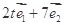 与向量
与向量 的夹角余弦值为非负值,求实数
的夹角余弦值为非负值,求实数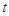 的取值范围.
的取值范围.
已知函数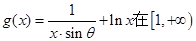 上为增函数,且
上为增函数,且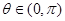 ,
, ,
, .
.
(1)求 的值;
的值;
(2)当 时,求函数
时,求函数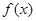 的单调区间和极值;
的单调区间和极值;
(3)若在 上至少存在一个
上至少存在一个 ,使得
,使得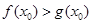 成立,求
成立,求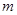 的取值范围.
的取值范围.