如图所示,轻杆AB长 ,两端各连接A、B小球,质量均为m,杆可以绕距B端1/3处的O轴在竖直平面内自由转动。轻杆由水平位置从静止开始转到竖直方向,求:
,两端各连接A、B小球,质量均为m,杆可以绕距B端1/3处的O轴在竖直平面内自由转动。轻杆由水平位置从静止开始转到竖直方向,求: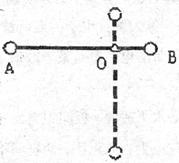
(1)此过程中杆对A球做的功是多少。
(2)在竖直方向时转轴O受的作用力大小及方向.(重力加速度为g,不计g一切阻力)
一条圆柱形的光导纤维长为L、折射率为n,光在真空中的传播速度为c,求:光从它的一端端面的圆心射入,经全反射后从另一端射出,所需的最长时间t。
一个密闭的气缸内的理想气体被活塞分成体积相等的左右两室,气缸壁与活塞都是不导热的,活塞与气缸壁之间没有摩擦。开始时,左右两室中气体的温度相等,如图所示。现利用左室中的电热丝对左室中的气体加热一段时间。达到平衡后,左室气体的体积变为原来体积的1.5倍,且右室气体的温度变为300 K。求加热后左室气体的温度。(忽略气缸、活塞的热胀冷缩)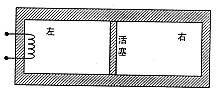
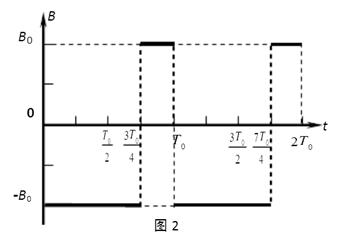
真空中有如图l装置,水平放置的金属板A、B中间开有小孔,小孔的连线沿竖直放置的金属板C、D的中间线,一质量为m、电荷量为q的带正电粒子(初速不计、重力不计)P进入A、B间被加速后,再进入金属板C、D间的偏转电场偏转,并恰能从D板下边缘射出。已知金属板A、B间电势差为UAB=+U0,C、D板长度均为L,C、D板间距为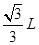 。在金属板C、D下方有如图l所示的、有上边界的、范围足够大的匀强磁场,该磁场上边界与金属板C、D下端重合,其磁感应强度随时间变化的图象如图2,图2中的B0为已知,但其变化周期T未知,忽略偏转电场的边界效应。
。在金属板C、D下方有如图l所示的、有上边界的、范围足够大的匀强磁场,该磁场上边界与金属板C、D下端重合,其磁感应强度随时间变化的图象如图2,图2中的B0为已知,但其变化周期T未知,忽略偏转电场的边界效应。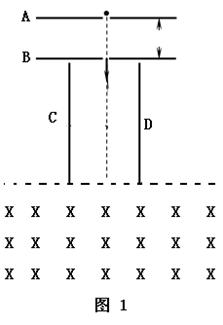
(1)求金属板C、D间的电势差UCD;
(2)求粒子刚进入磁场时的速度;
(3)已知垂直纸面向里的磁场方向为正方向,该粒子在图2中t=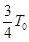 时刻进入磁场,并在t=T0时刻的速度方向恰好水平,求该粒子从射入磁场到离开磁场的总时间t总。
时刻进入磁场,并在t=T0时刻的速度方向恰好水平,求该粒子从射入磁场到离开磁场的总时间t总。
如图所示,一足够长的固定斜面与水平方向的夹角为θ=37°,物体B与斜面间的动摩擦因数为μ=0.5。将物体A以初速度v0从斜面顶端水平抛出的同时,物体B在斜面上距顶端L= 16.5 m处由静止释放,经历时间t,物体A第一次落到斜面上时,恰与物体B相碰,已知sin37°= 0.6,cos37°= 0.8,g=10m/s2,不计空气阻力,两物体都可视为质点。求:v0和t的大小。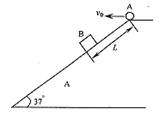
如图所示,质量M="2" kg的小车静一止在光滑的水平面上,车面上AB段是长L="1" m的光滑水平平面,与AB相切的BC部分是半径为R=0.3 m的光滑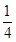 圆弧轨道,今有一质量m=1kg的小金属块以水平初速度v0从A端冲上AB面,恰能上升到
圆弧轨道,今有一质量m=1kg的小金属块以水平初速度v0从A端冲上AB面,恰能上升到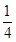 圆弧轨道的最高点C,求初速度v0的大小。(取g="1" 0m/s2)
圆弧轨道的最高点C,求初速度v0的大小。(取g="1" 0m/s2)