某商家经销一种绿茶,用于装修门面已投资3000元。已知绿茶每千克成本50元,在第一个月的试销时间内发现。销量w(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示
| 销售单价x(元/ kg) |
…… |
70 |
75 |
80 |
85 |
90 |
…… |
| 销售量w(kg) |
…… |
100 |
90 |
80 |
70 |
60 |
…… |
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量-成本-投资)。
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700,那么第二个月时里应该确定销售单价为多少元?
如图,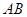 是
是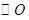 的直径,弦
的直径,弦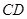 ⊥
⊥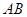 于点
于点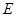 ,
,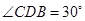 ,
,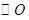 的半径
的半径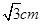 ,则弦
,则弦 的长为多少?
的长为多少?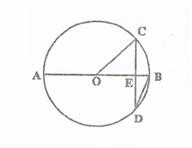
解不等式组 ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
化简求值: ,其中
,其中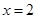 .
.
在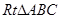 中,
中, ,
, ,
,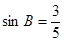 ,⊙
,⊙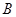 的半径长为1,⊙
的半径长为1,⊙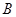 交边
交边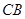 于点
于点 ,
,
点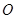 是边
是边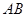 上的动点.
上的动点.
(1)如图1,将⊙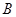 绕点
绕点 旋转
旋转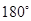 得到⊙
得到⊙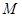 ,请判断⊙
,请判断⊙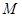 与直线
与直线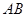 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求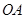 的长;
的长;
(3)如图3,点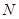 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙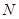 和以
和以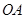 为半径的⊙
为半径的⊙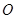 外切,设
外切,设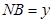 ,
, ,求
,求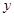 关于
关于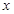 的函数关系式及定义域..
的函数关系式及定义域..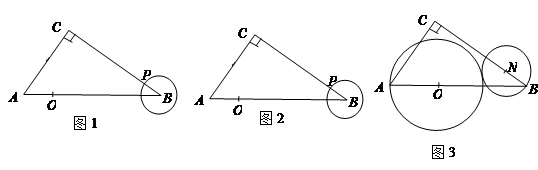
函数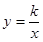 和
和
 的图像关于
的图像关于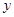 轴对称,我们把函数
轴对称,我们把函数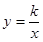 和
和
 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数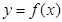 和
和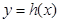 的图像关于
的图像关于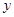 轴对称,那么我们就把函数
轴对称,那么我们就把函数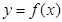 和
和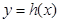 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数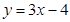 的“镜子”函数:,
的“镜子”函数:,
(2)函数的“镜子”函数是 ;
;
(3)如图7,一条直线与一对“镜子”函数 (
(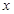 >
>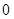 )和
)和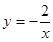 (
(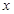 <
<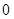 )的图像分别交于点
)的图像分别交于点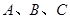 ,如果
,如果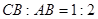 ,点
,点 在函数
在函数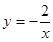 (
(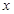 <
<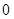 )的“镜子”函数上的对应点的横坐标是
)的“镜子”函数上的对应点的横坐标是 ,求点
,求点 的坐标.
的坐标.