如图,抛物线与x轴相交于B,C两点,与y轴相交于点A,点P(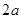 ,
,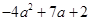 )(a是任意实数)在抛物线上,直线
)(a是任意实数)在抛物线上,直线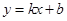 经过A,B两点.
经过A,B两点.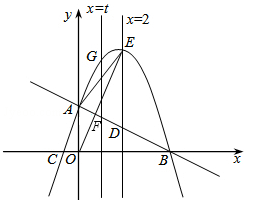
(1)求直线AB的解析式;
(2)平行于y轴的直线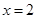 交直线AB于点D,交抛物线于点E.
交直线AB于点D,交抛物线于点E.
①直线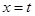 (0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
(0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
②将抛物线向上平移m(m>0)个单位,当EO平分∠AED时,求m的值.
两会期间,环保问题受到与会代表的广泛关注.近期多地纯电动出租车正式上路运行,下表是普通燃油出租车和纯电动出租车的运价.
| 车型 |
起步公里数 |
起步价格 |
超出起步公里数后的单价 |
| 普通燃油型 |
3 |
9元+2元(燃油附加费) |
2.4元/公里 |
| 纯电动型 |
2.5 |
9元 |
2.9元/公里 |
设乘客打车的路程为x公里,乘坐普通燃油出租车及纯电动出租车所需费用分别为y1、y2元.
(1)直接写出y1、y2关于x的函数关系式,并注明对应的x的取值范围;
(2)在如下的同一个平面直角坐标系中,画出y1、y2关于x的函数图象;
(3)结合图象,求出当乘客打车的路程在什么范围内时,乘坐纯电动出租车更合算.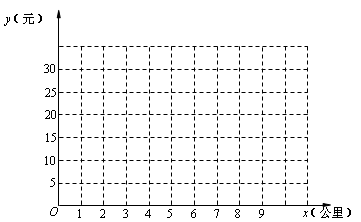
小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过10件,单价为80元:如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元.按此优惠条件,小丽一次性购买了这种服装x件.
(1)当x=12时,小丽购买的这种服装的单价为;
(2)小丽一次性购买这种服装付了1200元.请问她购买了多少件这种服装?
图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN.我们把∠ANB叫做倾斜角.
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
如图,⊙O是△ABC的外接圆,AB=AC,P是⊙O上一点.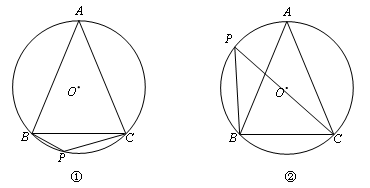
(1)请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)结合图②,说明你这样画的理由.
近期,中国足球改革方案由中央深改小组审议通过,中国足球迎来春天的气息.甲、乙、丙三人进行踢足球训练.球从一个人脚下随机传到另外一个人脚下,共传球三次.
(1)若开始时球在甲脚下,求经过三次传球后,球传回甲脚下的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己脚下的概率最大,乙会让球开始时在谁脚下?请说明理由.