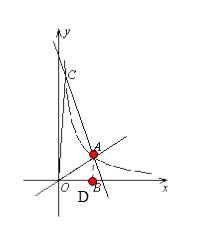
如图,O是坐标原点,直线OA与双曲线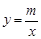 在第一象限内交于点A,过点A的直线
在第一象限内交于点A,过点A的直线 与x轴正半轴交于点B,与双曲线的另一交点为C,连结OC. 若
与x轴正半轴交于点B,与双曲线的另一交点为C,连结OC. 若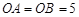 ,
,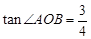 .
.
(1)求双曲线和直线AB的解析式;
(2)求△AOC的面积.
(3)在第一象限内,根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点 ,用测角仪测出看塔顶
,用测角仪测出看塔顶 的仰角
的仰角 ,在
,在 点和塔之间选择一点
点和塔之间选择一点 ,测出看塔顶
,测出看塔顶 的仰角
的仰角 ,然后用皮尺量出
,然后用皮尺量出 .
. 两点的距离为
两点的距离为 m,自身的高度为
m,自身的高度为 m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度( ,结果保留整数).
,结果保留整数).
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影 的长为
的长为 m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是:;
②要计算出塔的高,你还需要测量哪些数据?.
小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
为实现区域教育均衡发展,我市计划对某县 、
、 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所 类学校和两所
类学校和两所 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所 类学校和一所
类学校和一所 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所 类学校和一所
类学校和一所 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的 类学校不超过5所,则
类学校不超过5所,则 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县 、
、 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到 、
、 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,
轴于点E, .
.
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
某区从参加初中八年级数学调研考试的8000名学生成绩中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得到表一;随后汇总整个样本数据,得到表二.
请根据表一、表二所提供的信息,回答下列问题:
(1)样本中,学生数学成绩平均分约为分(结果精确到0.1);
(2)样本中,数学成绩在84≤x<96分数段的频数为,等级为A的人数占抽样学生总数的百分比为,中位数所在的分数段为;