如图所示，平面直角坐标系xoy中，在第二象限内有竖直放置的两平行金属板，其中右板开有小孔；在第一象限内存在内、外半径分别为
、R的半圆形区域，其圆心与小孔的连线与x轴平行，该区域内有磁感应强度为B的匀强磁场，磁场的方向垂直纸面向里：在y<0区域内有电场强度为E的匀强电场，方向与x轴负方向的夹角为60°。一个质量为m，带电量为－q的粒子（不计重力），从左金属板由静止开始经过加速后，进入第一象限的匀强磁场。求:
（1）若两金属板间的电压为U，粒子离开金属板进入磁场时的速度是多少?
（2）若粒子在磁场中运动时，刚好不能进入的中心区域，此情形下粒子在磁场中运动的速度大小。
（3）在（2）情形下，粒子运动到y<0的区域，它第一次在匀强电场中运动的时间。
如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体。活塞的质量为m，横截面积为S，与容器底部相距h，此时封闭气体的温度为T1。现通过电热丝缓慢加热气体，当气体吸收热量Q时，气体温度上升到T2。已知大气压强为p0，重力加速度为g，不计活塞与气缸的摩擦，求：
①活塞上升的高度；
②加热过程中气体的内能增加量。
如图所示，两根相同的平行金属直轨道竖直放置，上端用导线接一定值电阻，下端固定在水平绝缘底座上。底座中央固定一根弹簧，金属直杆ab通过金属滑环套在轨道上。在MNPQ之间分布着垂直轨道面向里的匀强磁场，现用力压杆使弹簧处于压缩状态，撤力后杆被弹起，脱离弹簧后进入磁场，穿过PQ后继续上升，然后再返回磁场，并能从边界MN穿出，此后不再进入磁场。杆ab与轨道的摩擦力大小恒等于杆重力的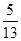
倍。已知杆向上运动时，刚穿过PQ时的速度是刚穿过MN时速度的一半，杆从PQ上升的最大高度（未超过轨道上端）是磁场高度的n倍；杆向下运动时，一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻，已知重力加速度为g。求：
（1）杆向上穿过PQ时的速度与返回PQ时的速度大小之比v1：v2；
（2）杆向上运动刚进入MN时的加速度大小a；
（3）杆向上、向下两次穿越磁场的过程中产生的电热之比Q1：Q2。
如甲图所示，长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处平滑连接，有一质量为2kg的滑块，从A处由静止开始受水平向右的力F作用，F与位移x的关系按乙图所示规律变化，滑块与AB和BC间的动摩擦因数均为0.5，重力加速度g取l0m/s2。求：
（1）滑块第一次到达B处时的速度大小；
（2）不计滑块在B处的速率变化，滑块到达B点时撤去力F，滑块冲上斜面，则滑块最终静止的位置与B点的距离多大。（sin37°=0.6）
如图所示，质量均为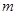
的物体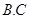
分别于轻质弹簧的两端栓接，将它们放在倾角为
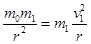=30°的光滑斜面上，静止时弹簧的形变量为x0．斜面底端有固定挡板D，物体C靠在挡板D上．将质量也为m的物体A从斜面上的某点由静止释放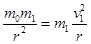，与B相碰．已知重力加速度为g，弹簧始终处于弹性限度内，不计空气阻力．求：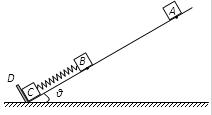
（1）弹簧的劲度系数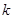
；
（2）若A与B相碰后粘连在一起开始做简谐运动，且A与B第一次运动达到最高点时，C对挡板D的压力恰好为0，求此简谐运动的振幅；
（3）若将A从另一位置由静止释放，A与B相碰后不粘连，但仍立即一起运动，且当B第一次运动到最高点时，C对挡板D的压力也恰好为零．已知A与B相碰后弹簧第一次恢复原长时B的速度大小为
，求相碰后A第一次运动达到的最高点与开始静止释放点之间的距离．
如图所示，两平行导轨间距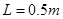
，足够长光滑的倾斜部分和粗糙的水平部分圆滑连接，倾斜部分与水平面的夹角
，垂直斜面方向向上的匀强磁场磁感应强度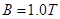
，水平部分没有磁场，金属杆
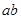质量
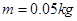，电阻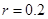
Ω，运动中与导轨始终接触良好，并且垂直于导轨。电阻
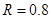Ω，导轨电阻不计。当金属棒从斜面上距底面高
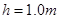以上的任何地方由静止释放后，在水平面上滑行的最大距离
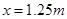，取
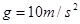，求：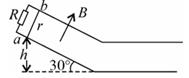
（1）金属棒在斜面上的最大运动速度；
（2）金属棒与水平导轨间的动摩擦因素；
（3）若金属棒从高度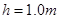处由静止释放，电阻
产生的热量.