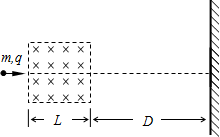如图所示,两根足够长的光滑金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角。完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止。取g=10m/s2,问:
(1)通过cd棒的电流I是多少,方向如何?
(2)棒ab受到的力F多大?
(3)力F的功率P是多少?
如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5T,还有沿x轴负方向的匀强电场,场强大小为E=2N/C.在其第一象限空间有沿y轴负方向的、场强大小也为E的匀强电场,并在y>h=0.4m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作匀速直线运动(PO与x轴负方向的夹角为θ=45O),并从原点O进入第一象限.已知重力加速度g=10m/s2,问:
①油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比,并指出油滴带何种电荷;
② 油滴在P点得到的初速度大小?③ 油滴在第一象限运动的时间。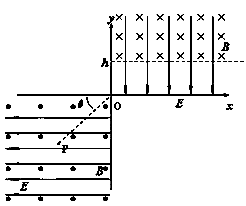
为了研究过山车的原理,某兴趣小组提出了下列设想:取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除 AB段以外都是光滑的。其AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿 AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数 μ = 0.50.(g=10m/s2、sin37°= 0.60、cos37° =0.80)
① 求小物块到达A点时速度。
② 要使小物块不离开轨道,并从轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件?
③ 为了让小物块不离开轨道,并且能够滑回倾斜轨道 AB,则竖直圆轨道的半径应该满足什么条件?
如图所示,质量为m,带电量为+q的微粒在0点以初速度v0与水平方向成q角射出,微粒在运动中受阻力大小恒定为f。
① 如果在某方向加上一定大小的匀强电场后,能保证微粒仍沿v0方向做直线运动,试求所加匀强电场的最小值的大小与方向。
③若加上大小一定,方向水平向左的匀强电场,仍能保证微粒沿vo方向做直线运动,并经过一段时间后又返回o点,求微粒回到o点时的速率。
一质量为1.0kg的物体从距地面180m的高处由静止开始下落,重力加速度g=10m/s2,忽略物体受到的空气阻力影响。求:
① 物体落到地面时的速度大小;
② 物体在空中运动的时间;
③ 物体下落的前3s内重力对物体做的功。
(12分)有一个正方体形的匀强磁场和匀强电场区域,它的截面为边长L=0.20m的正方形,其电场强度为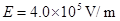 ,磁感应强度
,磁感应强度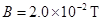 ,磁场方向水平且垂直纸面向里,当一束质荷比为
,磁场方向水平且垂直纸面向里,当一束质荷比为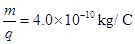 的正离子流(其重力和离子间相互作用不计)以一定的速度从电磁场的正方体区域的左侧边界中点射入,如图所示。(计算结果保留两位有效数字)
的正离子流(其重力和离子间相互作用不计)以一定的速度从电磁场的正方体区域的左侧边界中点射入,如图所示。(计算结果保留两位有效数字)
(1)要使离子流穿过电场和磁场区域而不发生偏转,电场强度的方向如何?离子流的速度多大?
(2)在上一问的情况下,在离电场和磁场区域右边界D=0.40m处有与边界平行的平直荧光屏。若只撤去电场,离子流击中屏上a点;若只撤去磁场,离子流击中屏上b点。求ab间距离。(a,b两点图中未画出)