(本小题满分14分)已知数列 中
中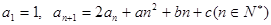 .
. 为实常数.
为实常数.
(Ⅰ)若 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若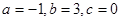 .
.
①是否存在常数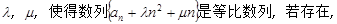 求出
求出 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②设 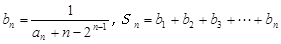 .证明:n≥2时,
.证明:n≥2时, .
.
已知椭圆 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率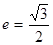 .
.
(1)求椭圆的方程;
(2)若点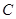 为曲线
为曲线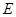 :
: 上任一点(
上任一点(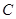 点不同于
点不同于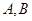 ),直线
),直线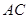 与直线
与直线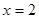 交于点
交于点 ,
,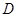 为线段
为线段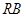 的中点,试判断直线
的中点,试判断直线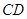 与曲线
与曲线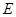 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
已知正项数列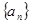 中,
中,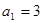 ,前n项和为
,前n项和为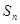
 ,当
,当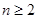 时,有
时,有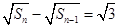 .(1)求数列
.(1)求数列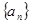 的通项公式;
的通项公式;
(2)记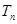 是数列
是数列 的前
的前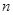 项和,若
项和,若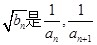 的等比中项,求
的等比中项,求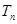 .
.
如图1,在直角梯形 中,
中,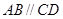 ,
,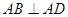 ,且
,且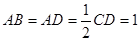 .
.
现以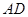 为一边向梯形外作正方形
为一边向梯形外作正方形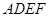 ,然后沿边
,然后沿边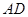 将正方形
将正方形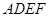 翻折,使平面
翻折,使平面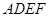 与平面
与平面 垂直,
垂直,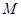 为
为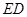 的中点,如图2.
的中点,如图2.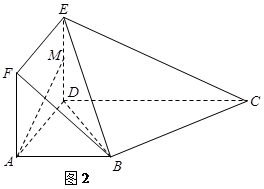
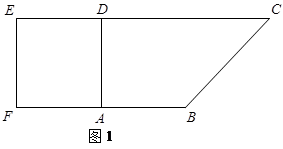
(1)求证: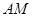 ∥平面
∥平面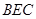 ;
;
(2)求证: ;
;
(3)求点 到平面
到平面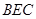 的距离.
的距离.
某校高三(1)班共有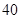 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在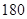 分钟到
分钟到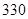 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:
| 组别 |
分组 |
频数 |
频率 |
| 第一组 |
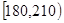 |
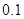 |
|
| 第二组 |
 |
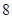 |
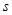 |
| 第三组 |
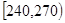 |
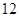 |
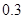 |
| 第四组 |
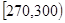 |
 |
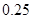 |
| 第五组 |
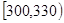 |
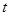 |
(1)求分布表中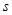 ,
,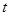 的值;
的值;
(2)王老师为完成一项研究,按学习时间用分层抽样的方法从这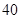 名学生中抽取
名学生中抽取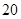 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?
(3)已知第一组学生中男、女生人数相同,在(2)的条件下抽取的第一组学生中,既有男生又有女生的概率是多少?
已知函数
(1)求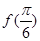 的值;
的值;
(2)若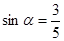 ,且
,且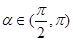 ,求
,求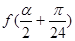 .
.