在数列 和
和 中,
中, ,
, ,
, ,其中
,其中 且
且 ,
, .
.
(Ⅰ)若 ,
, ,求数列
,求数列 的前
的前 项和;
项和;
(Ⅱ)证明:当 时,数列
时,数列 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;
(Ⅲ)设 ,
, ,试问在区间
,试问在区间 上是否存在实数
上是否存在实数 使得
使得 .若存在,求出
.若存在,求出 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合 ;若不存在,试说明理由.
;若不存在,试说明理由.
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
| 等级 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
a |
0.2 |
0.45 |
b |
c |
(1)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级编号为4的3件产品记为xl,x2,x3,等级编号为5的2件产品记为yl ,y2,现从xl,x2,x3,yl,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件品的级编号恰好相同的概率。
曲线 在点
在点 处的切线与x轴交点的横坐标为an.
处的切线与x轴交点的横坐标为an.
(1)求an;
(2)设 ,求数到
,求数到 的前n项和Sn.
的前n项和Sn.
已知数列 ,其前
,其前 项和
项和 ,数列
,数列 满足
满足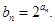
( 1 )求数列 、
、 的通项公式;
的通项公式;
( 2 )设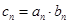 ,求数列
,求数列 的前
的前 项和
项和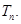
某水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本,预计产量每年递增1万件,每件水晶产品的固定成本 与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第 次投入后的年利润为
次投入后的年利润为 万元.
万元.
( 1 )求 的表达式;
的表达式;
( 2 )问从今年算起第几年利润最高?最高利润为多少万元?
设数列 的前
的前 项和为
项和为 ,
, 
( 1 )若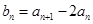 ,求
,求 ;
;
( 2 ) 若 ,证明
,证明 是等差数列.
是等差数列.