已知在数列{ }中,
}中,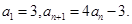
(1)求证:数列{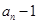 }是等比数列,并求出数列{
}是等比数列,并求出数列{ }的通项公式;
}的通项公式;
(2)设数列{ }的前竹项和为Sn,求Sn.
}的前竹项和为Sn,求Sn.
已知函数
(1)当a=1时,解不等式
(2)若存在 成立,求a的取值范围.
成立,求a的取值范围.
在极坐标系中,曲线 的极坐标方程为
的极坐标方程为 ,现以极点
,现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数)
为参数)
(1)写出直线l和曲线C的普通方程;
(2)设直线l和曲线C交于A,B两点,定点P(—2,—3),求|PA|·|PB|的值.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
已知函数 函数
函数 在
在 处取得极值1.
处取得极值1.
(1)求实数b,c的值;
(2)求 在区间[-2,2]上的最大值.
在区间[-2,2]上的最大值.