已知函数 函数
函数 在
在 处取得极值1.
处取得极值1.
(1)求实数b,c的值;
(2)求 在区间[-2,2]上的最大值.
在区间[-2,2]上的最大值.
在平面直角坐标系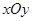 中,如图,已知椭圆E:
中,如图,已知椭圆E: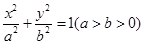 的左、右顶点分别为
的左、右顶点分别为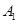 、
、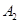 ,上、下顶点分别为
,上、下顶点分别为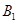 、
、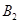 .设直线
.设直线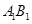 的倾斜角的正弦值为
的倾斜角的正弦值为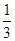 ,圆
,圆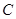 与以线段
与以线段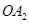 为直径的圆关于直线
为直径的圆关于直线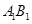 对称.
对称.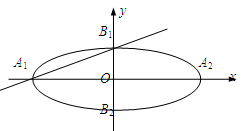
(1)求椭圆E的离心率;
(2)判断直线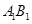 与圆
与圆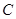 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆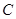 的面积为
的面积为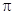 ,求圆
,求圆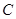 的方程.
的方程.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.
已知函数 .
.
(1)设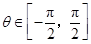 ,且
,且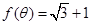 ,求
,求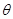 的值;
的值;
(2)在△ABC中,AB=1, ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值.
已知集合
 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为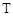 子集,记
子集,记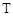 子集的个数为
子集的个数为 .
.
(1)当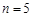 时,写出所有
时,写出所有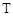 子集;
子集;
(2)求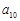 ;
;
(3)记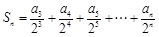 ,求证:
,求证: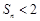
已知椭圆 过点
过点 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点 的直线
的直线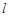 与椭圆
与椭圆 交于
交于 两点,且
两点,且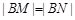 ,求直线
,求直线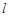 的方程.
的方程.