(本小题满分12分)
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.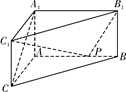
(1)求证:CA1⊥C1P;
(2)当AP为何值时,二面角C1-PB1-A1的大小为?
(本小题满分12分)
在高三年级某班组织的欢庆元旦活动中,有一项游戏规则如下:参与者最多有5次抽题并答题的机会.如果累计答对2道题,立即结束游戏,并获得纪念品;如果5次机会用完仍未累计答对2道题,也结束游戏,并不能获得纪念品.已知某参与者答对每道题答对的概率都是,且每道题答对与否互不影响.
(1)求该参与者获得纪念品的概率;
(2)记该参与者游戏时答题的个数为 ,求
,求 的分布列及期望
的分布列及期望
(本小题满分12分)
已知向量m=(sin,1),n=(cos,cos2),f(x)=m·n.
(1)若f(x)=1,求cos(-x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=- 是f(x)的极值点,求
是f(x)的极值点,求 f(x)在[1,a]上的最大值;
f(x)在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
已知数列{an}中,a1=1,当n≥2时,其前n项和Sn满足S =an(Sn-
=an(Sn- ).
).
(1)证明: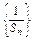 是等差数列,求Sn的表达式;
是等差数列,求Sn的表达式;
(2)设bn=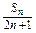 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.