已知四棱锥P—ABCD中, 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形, ,AB=
,AB= PA=2,E.F分别为B C.PD的中点。
PA=2,E.F分别为B C.PD的中点。
(Ⅰ)求证:PB//平面AFC;
(Ⅱ)求平面PAE与平面PCD所成锐二面角的余弦值。
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为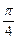 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
已知过点A(0,1),且方向向量为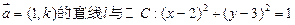 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数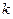 的取值范围;
的取值范围;
(2)求证: ;
;
(3)若O为坐标原点,且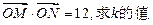 .
. 

设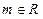 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量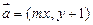 ,向量
,向量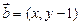 ,
,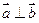 ,动点
,动点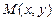 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状; 

(2)已知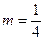 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且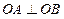 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知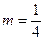 ,设直线
,设直线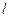 与圆C:
与圆C: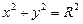 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且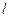 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
已知动圆过定点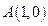 ,且与直线
,且与直线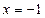 相切.
相切.
(1)求动圆的圆心轨迹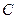 的方程;
的方程;
(2) 是否存在直线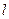 ,使
,使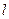 过点
过点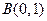 ,并与轨迹
,并与轨迹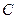 交于
交于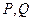 两点,
两点,
且满足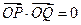 ?若存在,求出直线
?若存在,求出直线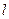 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知:以点C (t, )(t∈R , t≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.