已知函数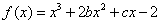 的图象在与
的图象在与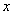 轴交点处的切线方程是
轴交点处的切线方程是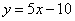 .
.
(Ⅰ)求函数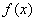 的解析式;
的解析式;
(Ⅱ)设函数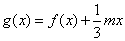 ,若
,若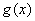 的极值存在,求实数
的极值存在,求实数 的取值范围以及当
的取值范围以及当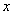 取何值时函数
取何值时函数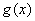 分别取得极大和极小值.
分别取得极大和极小值.
求圆心在直线x+y=0上,且过两圆x2+y2-2x+10y-24=0,x2+y2+2x+2y-8=0的交点的圆的方程.
已知圆C1:x2+y2-2mx+4y+m2-5="0," 圆C2: x2+y2+2x-2my+m2-3=0,当m为何值时,圆C1与圆C2相切?
判断圆C1:x2+y2-2x-6y-26=0与圆C2:x2+y2-4x+2y+4=0的公切线条数.
如图所示的是一座圆拱桥的示意图,当水面距拱顶2米时,水面宽12米,当水面下降1米后,水面宽为多少米? 
一台风中心在港口南偏东60°方向上,距离港口400千米处的海面上形成,并以每小时25千米的速度向正北方向移动,距台风中心350千米以内的范围将受到台风的影响,港口受到台风影响的时间为多少小时?