已知数列 满足
满足 ,且
,且 。
。
(1)求 。
。
(2)猜想数列 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
(本小题满分12分)设集合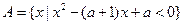 ,
,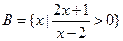 .
.
(1)当a=3时,求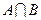 ;
;
(2)若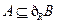 ,求a的取值范围.
,求a的取值范围.
(本小题满分13分)已知函数f (x) = 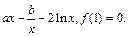
(1)若函数f (x)在其定义域内为单调函数,求实数a的取值范围;
(2)若函数f (x)的图象在x = 1处的切线垂直于y轴,数列{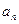 }满足
}满足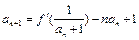 .
.
①若a1≥3,求证:an≥n + 2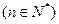 ;
;
②若a1 = 4,试比较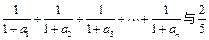 的大小,并说明你的理由.
的大小,并说明你的理由.
(本小题满分13分)某企业的产品以往专销欧美市场,在全球金融风暴的影响下,欧美市场的销量受到严重影响,该企业在政府的大力扶助下积极开拓国内市场,并基本形成了市场规模;自2009年9月以来的第n个月(2009年9月为第一个月)产品的内销量、出口量和销售总量(销售总量=内销量与出口量的和)分别为bn、cn和an(单位:万件),依据销售统计数据发现形成如下营销趋势:bn + 1 =" a" an,cn + 1 =" an" + b an2 (其中a、b为常数),已知a1 = 1万件,a2 = 1.5万件,a3 = 1.875万件.
(1)求a,b的值,并写出an + 1与an满足的关系式;
(2)试用你所学的数学知识论证销售总量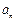 逐月递增且控制在2万件内;
逐月递增且控制在2万件内;
(3)试求从2009年9月份以来的第n个月的销售总量an关于n的表达式.
设函数 ,已知
,已知 ,且
,且 ,曲线
,曲线 在x=1处取极值.
在x=1处取极值.
|
(Ⅰ)如果函数 的递增区间为
的递增区间为 ,求
,求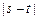 的取值范围;
的取值范围;
 是与
是与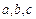 无关的常数
无关的常数 时,恒有
时,恒有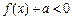 ,求实数
,求实数 的最小值
的最小值
(本小题满分12分)已知数列 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, .
.
(1)求数列 和
和 的通项公式
的通项公式
(2)数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.