如图,正方形 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ∥
∥ ,
, ,点
,点 在线段
在线段 上.
上.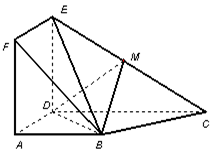
(I)当点 为
为 中点时,求证:
中点时,求证: ∥平面
∥平面 ;
;
(II)当平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥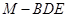 的体积.
的体积.
设实数x、y满足不等式组
(1)求点(x,y)所在的平面区域;
(2)设 ,在(1)所求的区域内,求函数
,在(1)所求的区域内,求函数 的最值
的最值
已知两点A(2,3)、B(4,1),直线l:x+2y-2=0,在直线l上求一点P.
(1)使|PA|+|PB|最小;
(2)使|PA|-|PB|最大.
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为 时,求弦AB的长.
时,求弦AB的长.
一圆与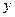 轴相切,圆心在直线
轴相切,圆心在直线 上,在
上,在 上截得的弦长为
上截得的弦长为 ,求此圆的方程.
,求此圆的方程.
已知长方形的四个顶点A(0,0)、B(2,0)、C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1<x4<2,求tanθ的取值范围.