已知长方形的四个顶点A(0,0)、B(2,0)、C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1<x4<2,求tanθ的取值范围.
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数: ,
, ,
,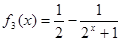 ,
,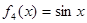 ,
,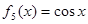 ,
,
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
在△ABC中,A、B、C的对边分别为a、b、c,向量 ,
,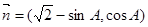 ,若
,若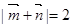 .
.
(1)求角A的大小;
(2)若 ,且
,且 ,求△ABC的面积
,求△ABC的面积
已知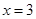 是函数
是函数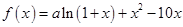 的一个极值点。
的一个极值点。
(1)求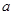 ;
;
(2)求函数 的单调区间;
的单调区间;
(3)若直线 与函数
与函数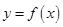 的图象有3个交点,求
的图象有3个交点,求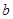 的取值范围
的取值范围
知函数 的图象在点
的图象在点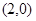 处的切线方程是
处的切线方程是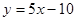 .
.
(1)求函数 的解析式;
的解析式;
(2)设函数 ,若
,若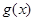 的极值存在,求实数
的极值存在,求实数 的取值范围
的取值范围
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格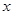 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式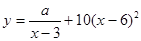 ,其中
,其中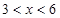 ,
,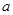 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求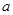 的值;
的值;
(2) 若该商品的成本为3元/千克, 试确定销售价格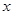 的值,使商场每日销售该商品所
的值,使商场每日销售该商品所
获得的利润最大.(利润=销售额-成本)