已知数列{ }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;
数列{ }满足:
}满足: -
-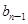 =
= (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.
(Ⅰ)求 和
和 ;
;
(Ⅱ)记数列 =
=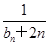 (n∈N﹡),若{
(n∈N﹡),若{ }的前n项和为
}的前n项和为 ,求
,求 .
.
如图,四棱柱 的底面
的底面 是平行四边形,
是平行四边形, 分别在棱
分别在棱 上,且
上,且 .
.
(1)求证: ;
;
(2)若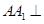 平面
平面 ,四边形
,四边形 是边长为
是边长为 的正方形,且
的正方形,且 ,
, ,求线段
,求线段 的长, 并证明:
的长, 并证明:

设函数 ,其中
,其中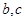 是某范围内的随机数,分别在下列条件下,求事件A “
是某范围内的随机数,分别在下列条件下,求事件A “ 且
且 ”发生的概率.
”发生的概率.
(1) 若随机数 ;
;
(2) 已知随机函数 产生的随机数的范围为
产生的随机数的范围为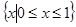 ,
, 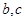 是算法语句
是算法语句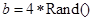 和
和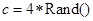 的执行结果.(注: 符号“
的执行结果.(注: 符号“ ”表示“乘号”)
”表示“乘号”)
在 中,角
中,角 为锐角,记角
为锐角,记角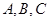 所对的边分别为
所对的边分别为 设向量
设向量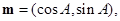
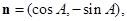 且
且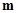 与
与 的夹角为
的夹角为
(1)求 的值及角
的值及角 的大小;
的大小;
(2)若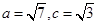 ,求
,求 的面积
的面积 .
.
已知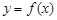 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
.
(1)求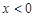 时,
时, 的解析式;
的解析式;
(2)问是否存在这样的非负数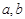 ,当
,当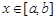 时,
时, 的值域为
的值域为 ?若存在,求出所有的
?若存在,求出所有的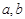 值;若不存在,请说明理由.
值;若不存在,请说明理由.
已知函数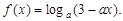
(1)当 时,函数
时,函数 恒有意义,求实数
恒有意义,求实数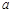 的取值范围;
的取值范围;
(2)是否存在这样的实数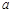 ,使得函数
,使得函数 在区间
在区间 上为减函数,并且最大值为1?如果存在,试求出
上为减函数,并且最大值为1?如果存在,试求出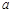 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.