已知圆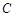 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线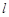 的参数方程是
的参数方程是 (
(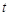 为参数)若直线
为参数)若直线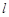 与圆
与圆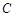 相切,求实数m的值.
相切,求实数m的值.
已知: .求证:
.求证: 中至少有一个不小于
中至少有一个不小于 .
.
已知函数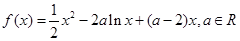 .
.
(Ⅰ)当a=1时,求函数 的最小值;
的最小值;
(Ⅱ)当a≤0时,讨论函数 的单调性;
的单调性;
(Ⅲ)是否存在实数a,对任意的x1,x2∈(0,+∞),且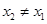 ,有
,有 ,恒成立,若存在求出a的取值范围,若不存在,说明理由.
,恒成立,若存在求出a的取值范围,若不存在,说明理由.
道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:
(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望,并指出所求期望的实际意义;
(Ⅲ)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的.依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率.(精确到0.01)并针对你的计算结果对驾驶员发出一句话的倡议.
某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如表.
| 优秀 |
非优秀 |
总计 |
|
| 课改班 |
50 |
||
| 非课改班 |
20 |
110 |
|
| 合计 |
210 |
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改有关”;
(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.
已知两个正数a,b满足a+b=1
(1)求证: ;
;
(2)若不等式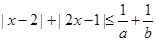 对任意正数a,b都成立,求实数x的取值范围.
对任意正数a,b都成立,求实数x的取值范围.