设 为整数,集合
为整数,集合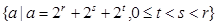 中的数由小到大组成数列
中的数由小到大组成数列 .(1)写出数列
.(1)写出数列 的前三项;(2)求
的前三项;(2)求 .
.
长度为 的线段AB的两个端点A、B在抛物线
的线段AB的两个端点A、B在抛物线 上运动,求AB中点到
上运动,求AB中点到 轴的最短距离。
轴的最短距离。
如图,在直四棱柱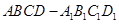 中,底面
中,底面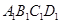 是梯形,且
是梯形,且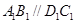 ,
,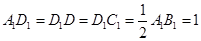 ,
,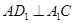 ,
, 是棱
是棱 的中点.
的中点.
(1)求证: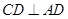 ;
;
(2)求点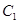 到平面
到平面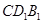 的距离;
的距离;
(3)求二面角 的大小.
的大小.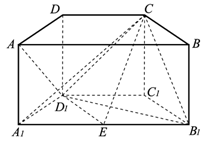
在五棱锥 中,
中,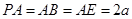 ,
,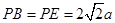 ,
,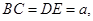

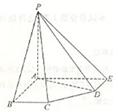
(1)求证: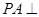 平面
平面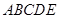 ;
;
(2)求二面角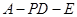 的大小;
的大小;
(3)求点C到平面PDE的距离.
平面上有两个质点A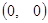 ,B
,B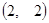 ,在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左,右移动的概率都是
,在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左,右移动的概率都是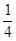 ,向上,下移动的概率分别是
,向上,下移动的概率分别是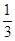 和
和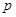 ,质点B向四个方向移动的概率均为
,质点B向四个方向移动的概率均为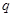 .(1)求
.(1)求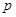 和
和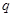 的值;(2)试判断至少需要几秒,A、B能同时到达D
的值;(2)试判断至少需要几秒,A、B能同时到达D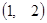 ,并求出在最短时间同时到达的概率?
,并求出在最短时间同时到达的概率?
甲、乙两人各射击1次,击中目标的概率分别是 和
和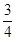 . 假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
. 假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则中止其射击. 问:乙恰好射击5次后,被中止射击的概率是多少?