学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球；乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖.（每次游戏结束后将球放回原箱）
（1）求在1次游戏中，
①摸出3个白球的概率；
②获奖的概率；
（2）求在两次游戏中获奖次数
的分布列及数学期望
.
已知函数f(x)＝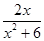
.
(1)若f(x)>k的解集为{x|x<－3，或x>－2}，求k的值；
(2)对任意x>0，f(x)≤t恒成立，求t的取值范围．
设向量a＝(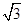
sin x，sin x)，b＝(cos x，sin x)，x∈
.
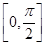(1)若|a|＝|b|，求x的值；
(2)设函数f(x)＝a·b，求f(x)的最大值．
已知复数z1满足(z1－2)(1＋i)＝1－i(i为虚数单位)，复数z2的虚部为2，且z1·z2是实数，求z2.
(1)如图所示，证明命题“a是平面π内的一条直线，b是π外的一条直线(b不垂直于π)，c是直线b在π上的投影，若a⊥b，则a⊥c”为真．
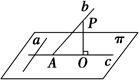
(2)写出上述命题的逆命题，并判断其真假(不需证明)．
已知p：|1－2x|≤5，q：x2－4x＋4－9m2≤0(m＞0)．若p是q的充分不必要条件，求实数m的取值范围．