设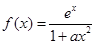
，其中a为正实数。
（1）当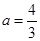
时，求
的极值点；
（2）若在R不是单调函数，求a的取值范围。
已知ABCD是平行四边形，P点是ABCD所在平面外的一点，连接PA、PB、PC、PD.设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.
（1）试用向量方法证明E、F、G、H四点共面；
（2）试判断平面EFGH与平面ABCD的位置关系，并用向量方法证明你的判断.
如图所示，正方体ABCD-A1B1C1D1，M为AA1的中点，N为A1B1上的点，且满足
A1N=
NB1，P为底面正方形A1B1C1D1的中心.求证：MN⊥MC，MP⊥B1C.
如图所示，平行六面体ABCD—A1B1C1D1中，以顶点A为端点的三条棱长度都为1，且两
两夹角为60°.
(1)求AC1的长；
（2）求BD1与AC夹角的余弦值.
如图所示,PD⊥平面ABCD,且四边形ABCD为正方形,AB=2,E是PB的中点,
cos〈
,
〉=
.
(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
如图所示，正四面体V—ABC的高VD的中点为O，VC的中点为M.
（1）求证：AO、BO、CO两两垂直；
（2）求〈
,
〉.